Motion generation

Motion generation plays an important role in robotics because it determines how a robot moves to accomplish its task. At its core, motion generation is about planning and executing trajectories that allow a robot to reach a desired position or follow a specific path, while taking into account constraints such as obstacles, joint limits, and safety requirements. This process is essential for enabling robots to perform useful work, whether it's picking up objects, assembling parts, or navigating safely through an environment.

One can differentiate between two approaches to motion generation; offline and online.

Offline motion generation plans trajectories in advance using models of the robot and environment. This method enables optimized, collision-free paths and is ideal for predictable, structured settings. Generated trajectories are rolled out in open loop, meaning that there is no feedback mechanism that would inform the system about disturbances. In other words, it lacks adaptability to real-time changes or sensor feedback. In the AICA System, the Joint Trajectory Controller often acts as simple offline motion generator, creating and rolling out a trajectory through a certain number of waypoints in a given amount of time without taking into account the environment.

Online motion generation computes movements in real time as the robot operates, allowing adaptation to dynamic environments and sensor input. This flexibility is essential for applications where the robot must be responsive and adaptive, such as working alongside humans, handling objects whose positions are not precisely known in advance, or when the task is highly driven by sensor feedback. Most often, such systems are closed loop, meaning that the current state of the robot and/or the environment is used to inform what to do next. The downside of this approach is that it often demands more computational resources and may not always find the most optimal path.

The choice between offline and online motion generation depends on the requirements of the application. In many cases, a combination of both approaches is used:

• either an initial trajectory is planned offline, and then online adjustments are made as needed to handle changes or uncertainties in the environment,
• or the task is divided into motions that simply move the robot from one point to another using fast and optimized trajectories and complex behaviors where the desired robot state is recomputed and adapted online.

AICA Core comes with several online motion generator components that use the current state of the robot to calculate the next command using a mathematical concept called Dynamical Systems.

Dynamical Systems

Dynamical System (DS) based closed loop control generates motion commands based on the current state of the robot or environment, rather than as a function of time, and is an effective way to generate reactive motion policies that generalize well to the robotic workspace while retaining stability guarantees. A first order, time invariant DS can be expressed as a differential equation

$$\frac{\mathrm{d}}{\mathrm{d}t}x = \dot x = f(x), x \in \R^n.$$

This equation says that the rate of change of the state, e.g. the velocity $\dot x$ of the state, is purely a function of the current state $x$, for all states $x$. In other words, the function $f(x)$ generates a motion direction from the instantaneous position of the robot, independent of time. The time-independence is a crucial point that makes such systems very capable for reactive motion generation. As offline trajectories are commonly parameterized over time, any disturbances or changes in target will either require replanning or result in failure of the execution because the system detects a deviation from the desired path. On the other hand, a DS is able to reject such disturbances because at any point in space, it still knows where to go next in order to reach the target.

The function $f(x)$ that defines the behavior of a DS can be implemented analytically from mathematical rules or optimized from a set of non-linear functions. The AICA component library includes examples of both kinds of behaviors.

tip

Dynamical Systems for robotic motion planning are an active area of scientific research, with ongoing work focused on improving adaptability, robustness, and learning Dynamical Systems from real world data. More on this topic can be found online.

Point Attractor Dynamical System

In a Point Attractor DS, the motion is always directed toward a specific point in space, known as the attractor. Regardless of where the state of the system is initialized, it will be drawn toward the attractor in a straight line, the strength of the attraction being proportional to the distance to the attractor. The differential equation of this DS can be written as

$$\dot x = f(x) = K(x^{\ast} - x), x \in \R^n,$$

where $x^{\ast}$ represents the attractor, and $K$ is an additional scaling constant. The figures below show the response of such a DS in 2D and 3D. It can be observed that all arrows point directly at the attractor, and the arrows become longer the further they are from the attractor, indicating a greater magnitude of attraction.

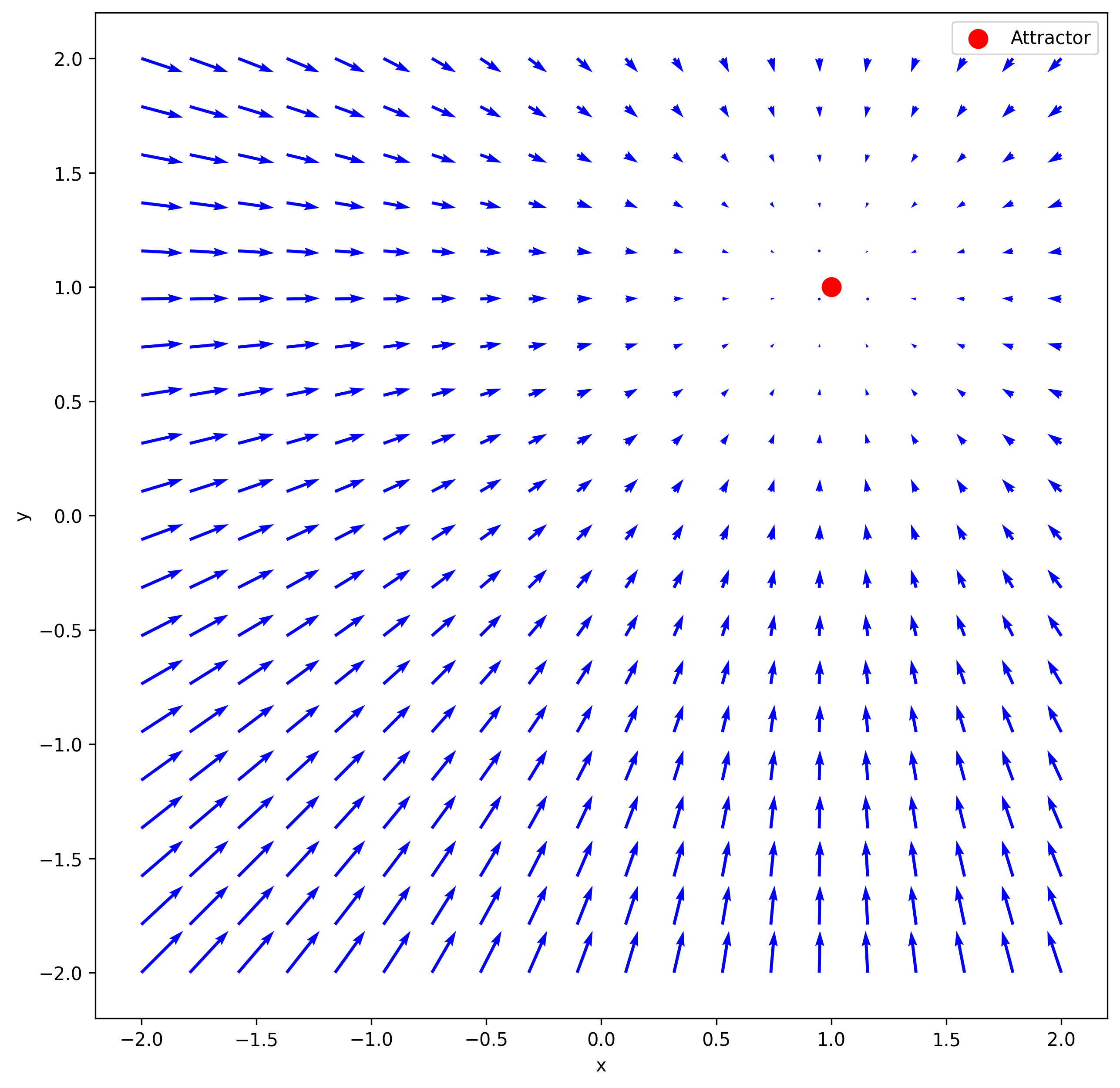
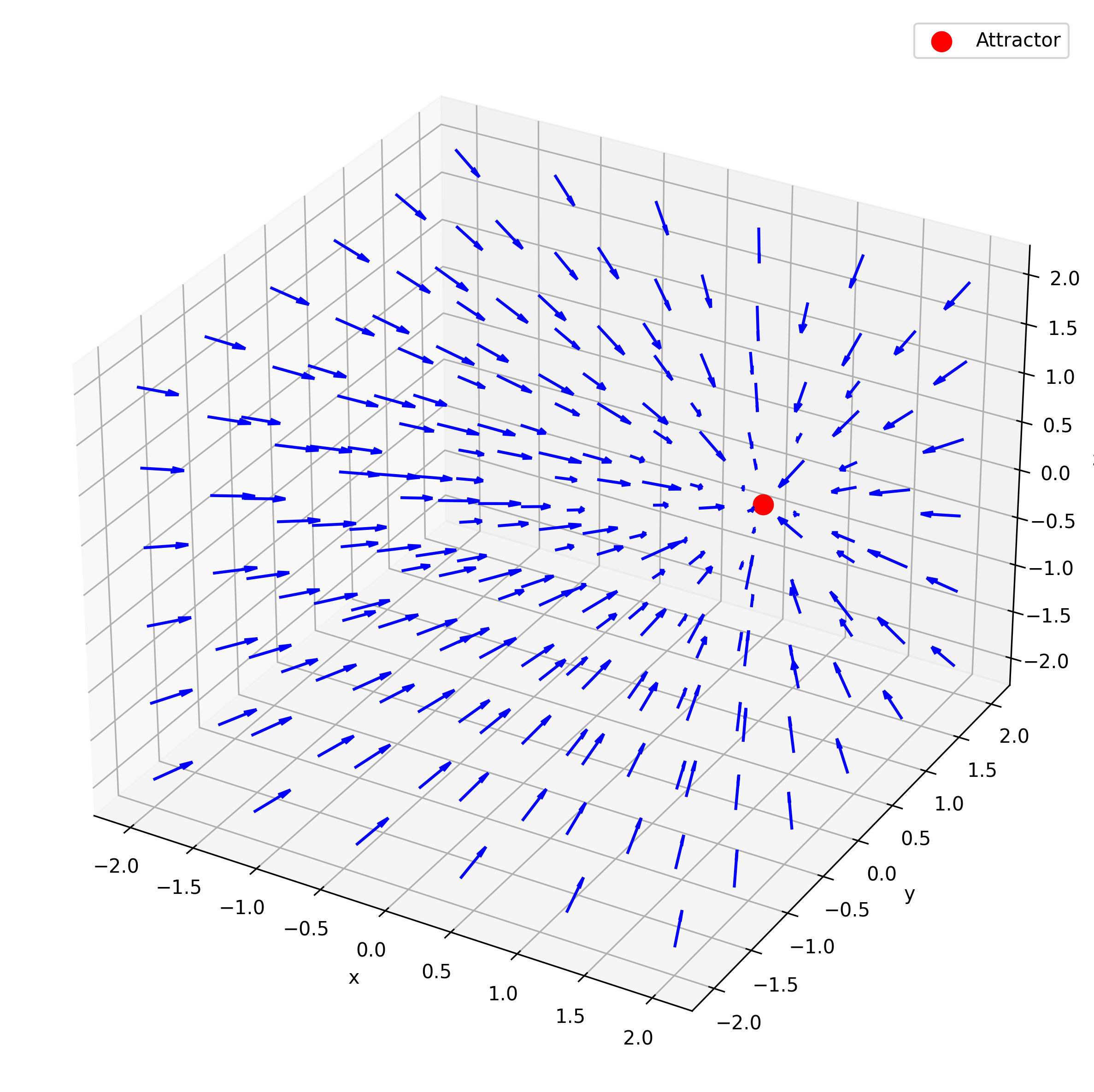
Point Attractor DS are especially useful for tasks like reaching or positioning, as they provide stable and predictable convergence to a (potentially moving) desired goal.

Stable Estimator of Dynamical Systems

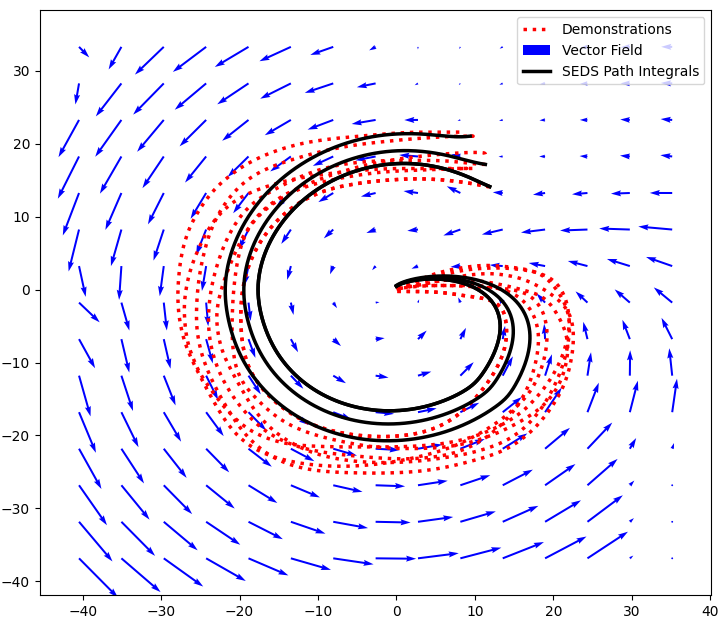
A Stable Estimator of Dynamical Systems (SEDS) is a method for learning dynamical systems from demonstration data while guaranteeing stability toward a target. SEDS models the provided example motions as a combination of several simple patterns, each represented by a Gaussian distribution. By using a mixture of Gaussians, SEDS can capture complex behaviors and make is possible to learn smooth and reliable movements from real world data. this makes it a powerful tool for task like manipulation and human-robot interaction, where both adaptability and safety are important.